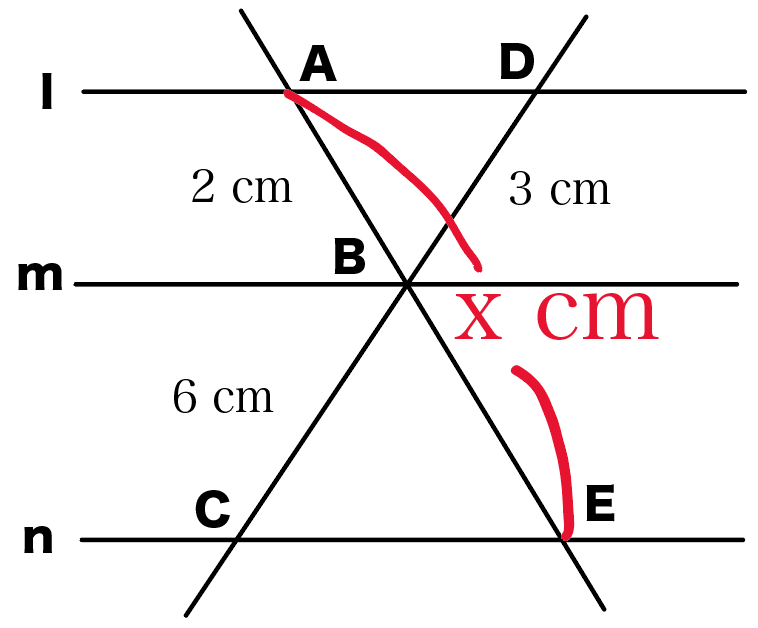
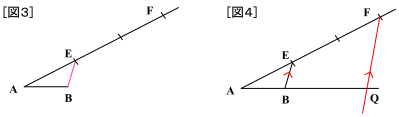
まず、平行線があるので、 最重要図形の1つである「砂時計型」に気づけるようになりましょう。 相似比は、 10 15 = 2 3 10 15 = 2 3 です。 対応する線分の比は 2 3 2 3 なので 下の図の赤い線分
線分の比と平行線 証明-相似_基礎 相似比と線分1 相似比と線分2 相似と線分比1(平行四辺形) 相似と線分比2 中点連結定理1 中点連結定理2 角の二等分線と辺の比1 角の二等分線と辺の比2 円と相似 相似比と線分の長さ(入試POINT:対応する線分の長さの比は、すべて等しい STEP 2 : A E O ∽ A B C ( B E O ∽ B A D でもOK) ③ ③ ⑤ A O A C = ③ ③ ⑤ = 3 8 (相似比) 3 8 = a これを解いて、 a = 15 2 STEP 3 :
線分の比と平行線 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  | |
 | ||
「線分の比と平行線 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
 |  | |
「線分の比と平行線 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「線分の比と平行線 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「線分の比と平行線 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「線分の比と平行線 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「線分の比と平行線 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 | ||
「線分の比と平行線 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  | |
「線分の比と平行線 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |
線分ab:線分acの長さの比が3:2なので 線分bdと線分cdの長さの比が3:2となります。(比が同じになる) したがって abdとacdの面積比は(高さが等しく底辺の長さの比が3:2なので)3:2と2 三角形の角の二等分線と辺の比には、内分と外分の2種類がある 21 内角の二等分線の定理と証明;
Incoming Term: 線分の比, 線分の比と面積比, 線分の比喩, 線分の比の定理, 線分の比と計量, 線分の比 三角形, 線分の比と平行線 証明, 線分の比と三角形の角の二等分線, 線分の比 高校, 線分の比の移動,




0 件のコメント:
コメントを投稿