対角線の長さが等しく、それぞれの中点で交わるとき長方形になる。 証明 それぞれの中点で交わるので四角形abcdは平行四辺形になる。 abcと dcbで 平行四辺形abcdの性質より ab=dc 1 bc=cb(共通) 2 仮定(対角線の長さが等しい)より② 平行線の性質や三角形の角についての性質を基にして,多角形の角についての性質が見いだせる ことを知る。 ③ 平面図形の合同の意味及び三角形の合同条件について理解する。 ④ 証明の必要性と意味及びその方法について理解する。 3 単元の評価規準質を証明することができる。 平行線と比の性質を使って、図形 の性質を考察し、それを証明する ことができる。 2 2 平行線と比 本・平行線と線分の比についての ・三角形と比の性質、中点連結定 時 定理を理解する。 理、平行線と比の性質を、相互に
Studydoctor平行線の性質と証明 中2数学 Studydoctor
平行線の性質 証明
平行線の性質 証明- 平行とは、交差せずに同一平面上にある直線です。 線が同じ平面上になく交差しない場合、それらは交差と呼ばれます。 線の平行度がその性質に基づいていることを証明します。 これは直接測定することによって行うことができます。 あなたが必要になりこんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定義とは まず、「平行四辺形とは何か」口で説明




高校数学 中線定理の5通りの証明 図形を扱う5分野の解法比較 受験の月
平行四辺形の性質と条件 4章 平行と合同(中2学年) 5 多角形の内角と外角 拡大、縮小 対頂角、平行線の性質と条件 相似な図形、相 図形の性質の調べ方 三角形の合同条件 平行線と線分の比 証明のしく1.対角線 ac をひく。 2.点 d を通り、ac に平行な直線 ℓ と、bc の延長との交点をm とする。 3.点 a , m を結んで abm をつくる。 証明 ア ac イ mac ウ abc 学 年 2年 図形の性質と証明⑩平行線と面積b 中学校数学・ワークブック 中学校数学 2b510bの新たな性質を証明する。 平行線と線分の比の定理を 見いだしそれを証明する。 三角形と比の定理や中点連三角形と比の定理や中点連 結定理,平行線と比の定理を結定理,平行線と比の定理 ををを 利用して線分の長さや新た な図形の性質を考える。
帰納的説明演繹的推論よる証明の違い理解いい。 目標 内容 ※太字次ページ詳細掲載 ・相似意味相似図形性質 ・三角形相似条件使た図形性質証明 ・平行線線分の比 ・中点連結定理 具体的問題通規則性見け三角形相 似条件既習図形性質用い証明必要性 理解・補助線4は,補助線2の証明と同じ考え方だ。 ・補助線5は,三角形の相似と平行線の性質を使う。これだけは, 三角形の比の定理を使わなくても証明できる。 ・補助線6は,どうやっていいかよく分からない。 ・相似な三角形を利用するためには,平行線平行線に挟まれている三角形は高さが等しい! というところです。 それでは、この性質を利用していろんな問題を解説していきますね。 台形の中から等しい三角形を見つける問題
1111 平行線の幾何(平行四辺形の定義と性質) 理一の数学事始め 21年8月8日 1940 フォローしました 平行四辺形 とは、2組の対辺が平行な四角形 (四辺形) のことである (※1)。 問題 平行四辺形が凸四角形であることを証明してください。 この問題に事例9 2年 図形の性質「三角形の合同の証明」 対頂角とその性質 平行 錯角,平行線の錯角 同位角,平行線の同位角 「それぞれ」の意味 平行になるための条件 ★三角形の合同条件を再確認しておくこ平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




これはどう証明すればいいのか 教えて下さい Clear
平行線における、①と▲の和は180度 (平行線公準)。 ▲と③の和も180度 (直線)なので①と③の角度は等しい。平行線と線分の 比についての性質 に関心をもち、平 行線の性質を三角 形の相似条件を用 いて証明しようと している。〔観察・ ノート〕 平行線と線分の 比についての性質 を,平行線の性質 や三角形の相似条 件を用いて証明す ることができる。 〔観察 平行線の公理より、点 A を通り直線 m に平行な直線は1つであるのに、直線 l と直線 l' の2本あることになり平行線の公理に反する。 α




高校受験入試で頻出 図形の基本と三角形の合同



数学的に 平行線が決して交わらないことをどのように証明できますか Quora
数学25章図形の性質と証明「平行四辺形の性質」<基本問題①・解答> (1) ①BCに平行な線を点Aから引く。 ②BAに平行な線を点Cから引く。 ③交わった点をDとする。 (2) ①点Cを通りBCに対して垂直な線を引く。歴史 平面上の互いに交わらない直線の対としての平行線の定義は『原論』第 i 巻の定義 23 に現れている 。 古代ギリシア人は、おもに平行線公準を証明しようと試みる中で、もっと別の平行線の定義についても議論している。 プロクルスは等距離直線としての平行線の定義はポセイドニオスに ただの位置関係しか示せなかった同位角が、証明のエースに化ける魔法の言葉です。 l と m は平行な直線です。 この場合、∠ a と∠ b の角の大きさは等しくなります。 そのことを平行線の同位角は等しいので、∠ a =∠ b と書きます。




高校数学 中線定理の5通りの証明 図形を扱う5分野の解法比較 受験の月




数学 平行線と面積 中学生 数学のノート Clear
平行線の錯角、同位角 平行線の定義・・・錯角の等しい2直線は平行である。 この定義から次の性質、条件が導ける。 平行線の性質 2つの直線に1つの直線が交わるとき、 2つの直線が 平行なら錯角は等しい 。 2つの直線が 平行なら同位角は等しい 。平行線と線分の比 1 課 題 平行線の性質をもとにして、生徒たちが調べたこ とをそれぞれ生徒に説明(証明)させるという課題 学習である。生徒一人一人が自分で課題を設定し、 自分の力で証明していくのであるから、学習内容は 生徒によって異なる。平行四辺形の性質について学んだあと、どのように証明問題を解けばいいのか解説していきます。 もくじ 1 平行四辺形の定義と4つの性質 11 2組の対辺の長さが等しい 12 2組の対角がそれぞれ等しい 121 対辺と対角が等しい証明 13 隣り合う角度を足す
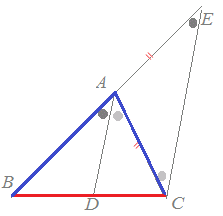



角の二等分線と補助線
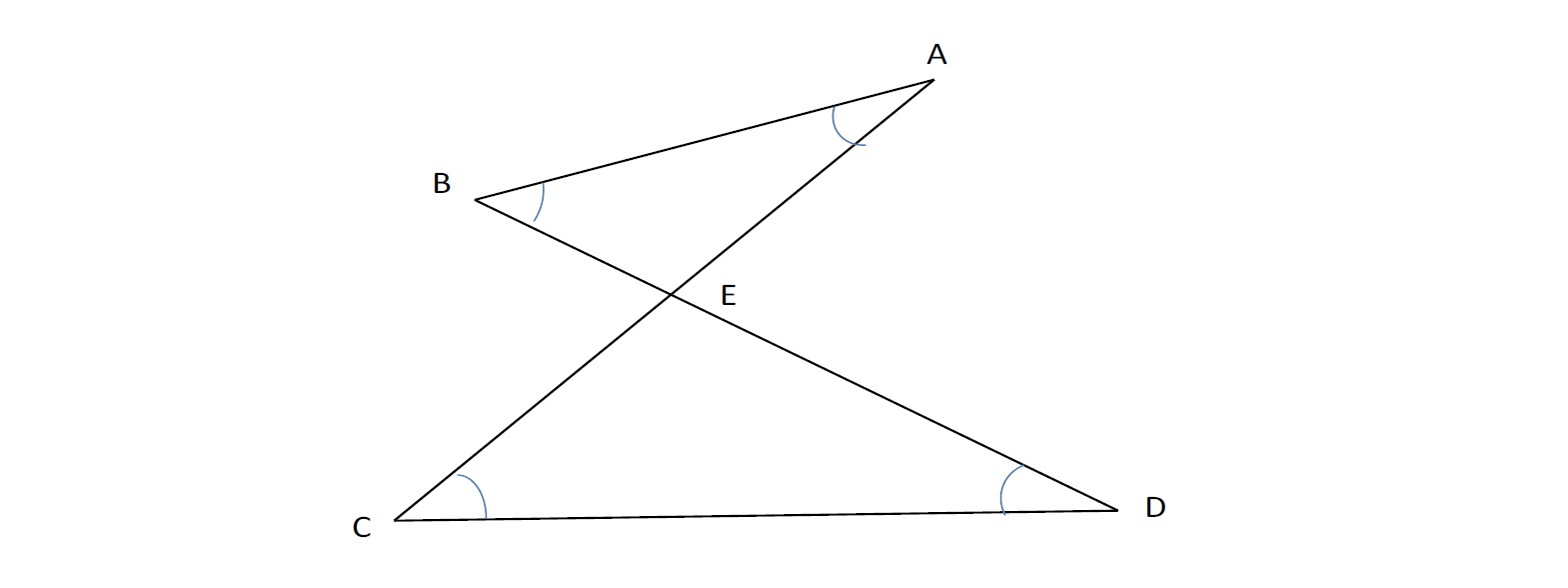



スリッパの法則 って 知っていますか ニッセイ基礎研究所
・平行線の性質などを数学の用語や記号を使って表したり,図形の性質の証明の過 程を説明したりすることができる。 ・平行線の性質などの基本的な図形の性質を理解するとともに,証明することの必 要性やしくみを理解することができる。平行四辺形abcd対角線の交点oを通る直線をひき、ab, cdとの交点をそれぞれe、fとすると、 oe=ofとなることを証明しましょう。 aeoと cfoにおいて 平行四辺形では、対角線はそれぞれの中点で交わるのでao=co・・・① ?ので∠aoe=∠cof・・・② 正解 :対頂角は等しい数学25章図形の性質と証明「平行線と面積」<応用問題> 組 番 名前 1右の図において,四角形ABCDは平行四辺形です。 このとき, BCFと面積が等しい三角形をすべて 答えなさい。 2右の図のように,平行四辺形ABCDの辺BC上に点E
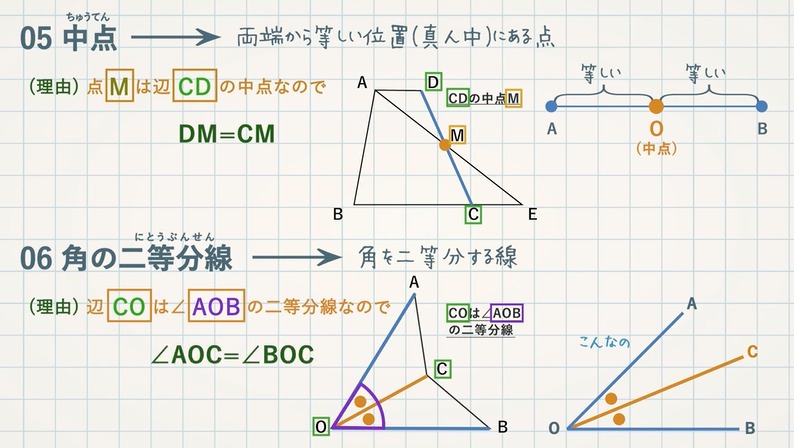



証明 合同 相似 が苦手な人へ 教遊者



平行四辺形の性質1
単元 平行と合同 1.単元の目標 (1)様々な事象を平行線の性質,三角形の角についての性質,三角形の合同条件などで捉えたり,平面図形の基本的な性質や関係を見いだしたりするなど,数学的に表現することに関心をもち,意欲的に問題解決に活用して考えたり判断したりしようとしている。まとめ対頂角の性質・平行線の性質・ 平行線になる条件を使えば,角と平行線の 問題が解決できる。 活動前時までの内容を確認し, 例題を全体で解決した後に,班で 問題演習をする。証明が必要な問 題は,随時解説をする。 まとめ平行線の第二次 平行線と線分の比の性質を,平行線の性質 ・証明の方針としてまとめるために,整 や三角形の相似条件を用いて証明する。(7) 理したことの間のつながりを考える。 ・証明としての形式的な表現等
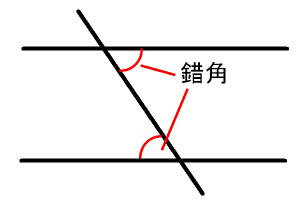



平行線と角




中2数学平行と合同についてです Clear
平行線の性質と証明中2数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・証明の手順に慣れよう ・平行線の性質を押さえておこう 完璧じゃなかったら授業動画を見よう やる気先生の授業動画平行四辺形の証明には対頂角や平行線などの性質の知識がいる 証明問題には対角線や垂線など今まで学んできたいろんな線が登場することが多いね。 ちょっと心配な人は「平行線と角」や「多角形の内角と外角」などの復習をしておこう。 多角形の内角学年 中学2年生, 単元 平行線と角,合同と証明, キーワード 中2,中2数学,数学,平行線,図形の性質,合同と証明,合同条件,数学A,math 中2数学図形の性質と証明 正三角形の性質 解説 3つの辺がすべて等しい三角形(定義)を正三角形といいます。




年度用 中学校数学教科書内容解説資料 未来へひろがる数学




平行線の性質を使った証明 Youtube
単元「図形の性質と証明」の小単元「平行線と面積」(2時間)における数学的活動を取り入れた授業モデルです。 下の授業展開案を授業にご活用ください。 単元 図形の性質と証明 (啓林館) 2 四角形平行線の性質 内容 2つの直線に1つの直線が交わるとき、次のことが成り立つ。 ①2つの直線が平行ならば、同位角は等しい。 ②2つの直線が平行ならば、錯角は等しい。 <戻る>2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。



Studydoctor平行線の性質と証明 中2数学 Studydoctor




平行線の性質の背理法による証明の過程から一つ Okwave
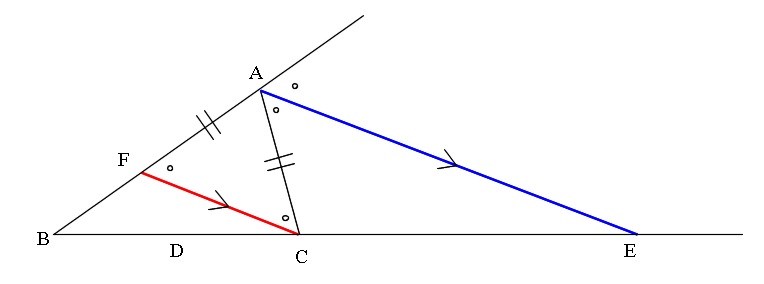



内角の二等分線と外角の二等分線の定理の覚え方と使い方
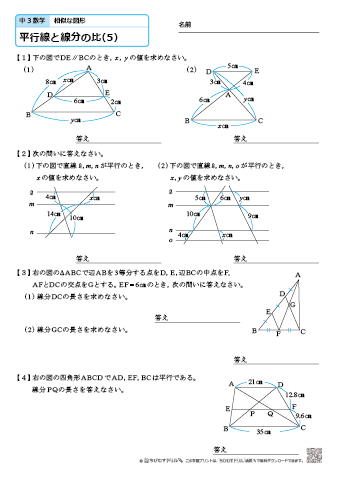



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
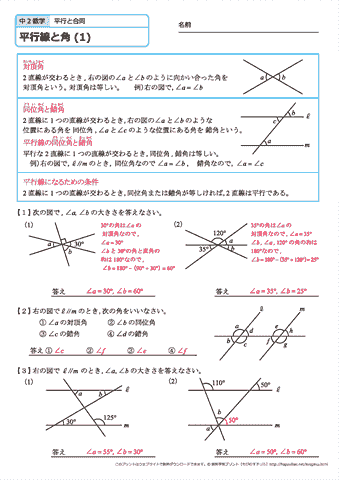



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角形の内角の和が180 になることの証明 数学fun




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張




中学数学 平面図形と平行線の性質



Q Tbn And9gcs8yek Ytk4aevkupzlfiomyr1swah7y0fxr8n2 Yhcmpzyumt Usqp Cau



1




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
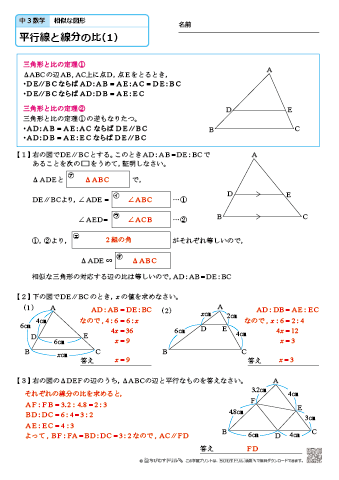



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
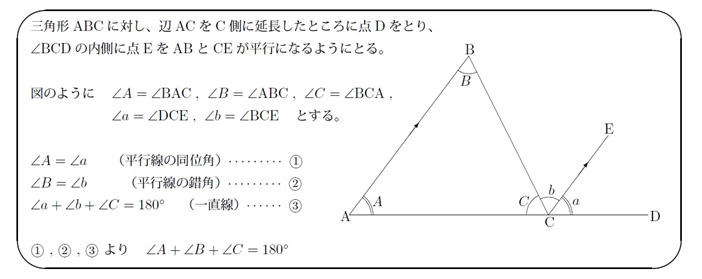



平行線の同位角 の証明 1 古代から数学者たちを悩ませ続けた 平行線公準 問題 アプロットの中高一貫校専門個別塾 大阪 谷町9丁目 上本町の個別指導塾




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
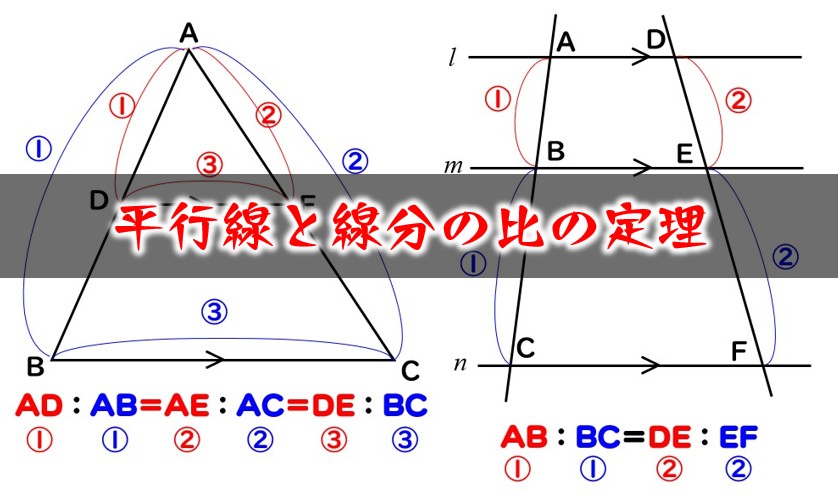



平行線と線分の比の定理 の問題の解き方 数学fun




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




中学数学 平行線と角 平行線の性質 Youtube
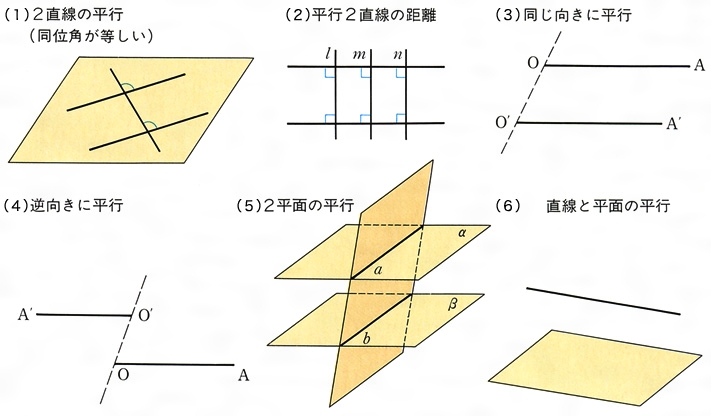



平行とは コトバンク
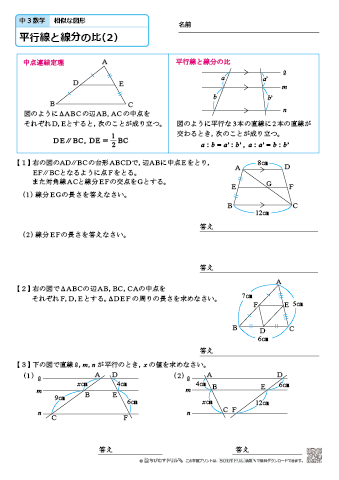



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
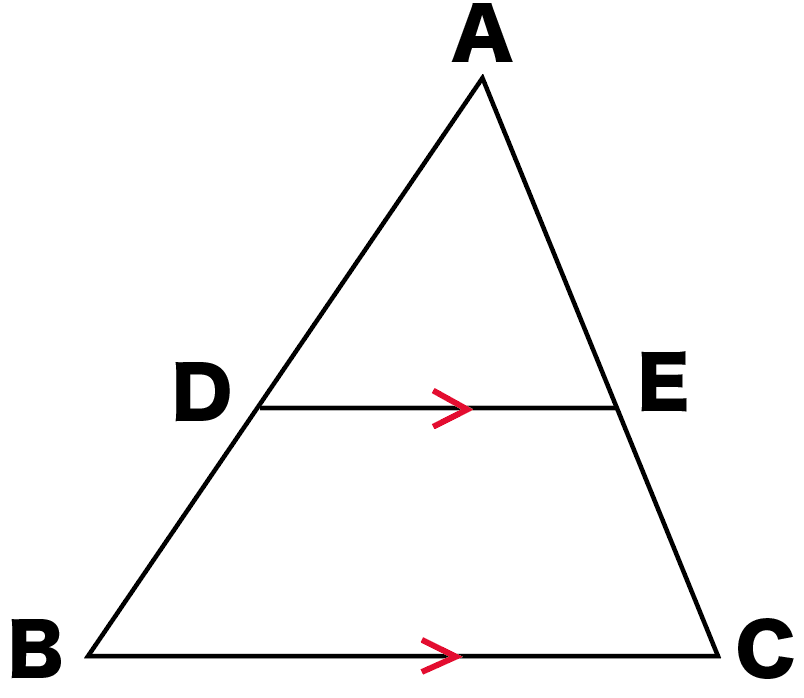



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




一番上の問題の Clear
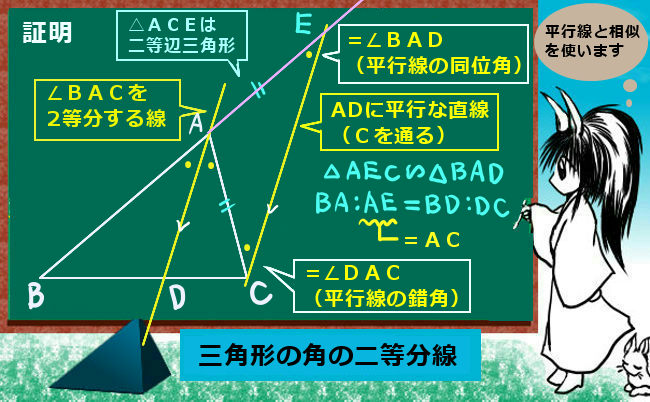



三角形の角の二等分線 理数系無料オンライン学習 Kori




平行線公準 Wikipedia




数学 平行と線分比をシッカリわかると メネラウスの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



1



1




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
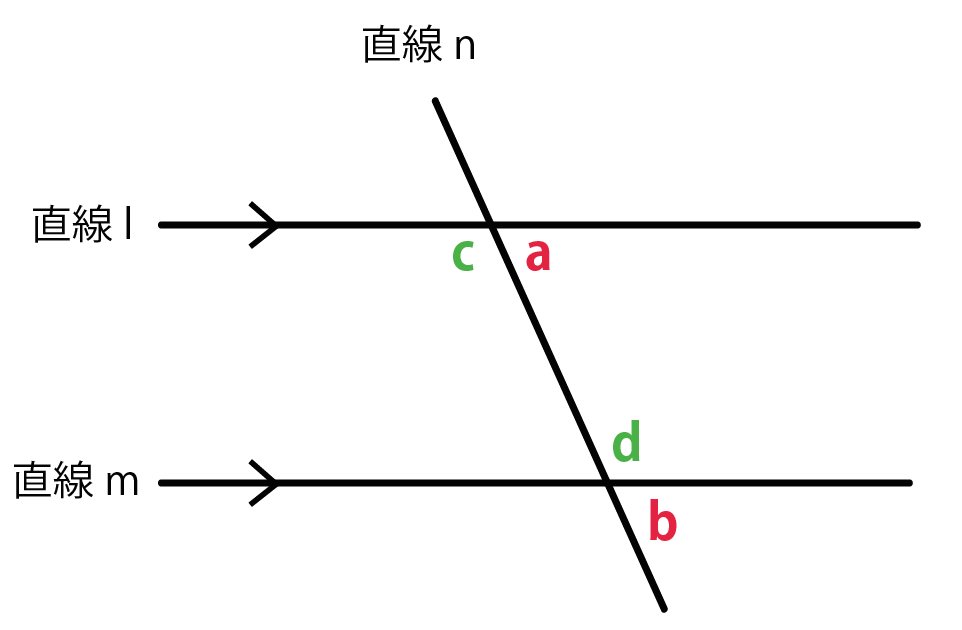



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく




第1巻命題29 平行線の錯角 同位角は等しい Stoixeia ストイケイア



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
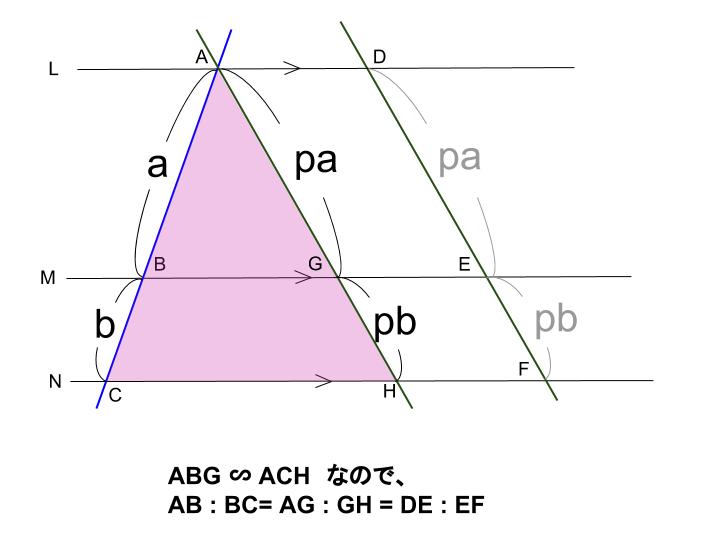



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su



三角形の角の二等分線定理 外角




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Studydoctor平行線の錯角と同位角 中学2年数学 Studydoctor



壮大 平行 の 定義




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




図形に関する性質の証明 身勝手な主張



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
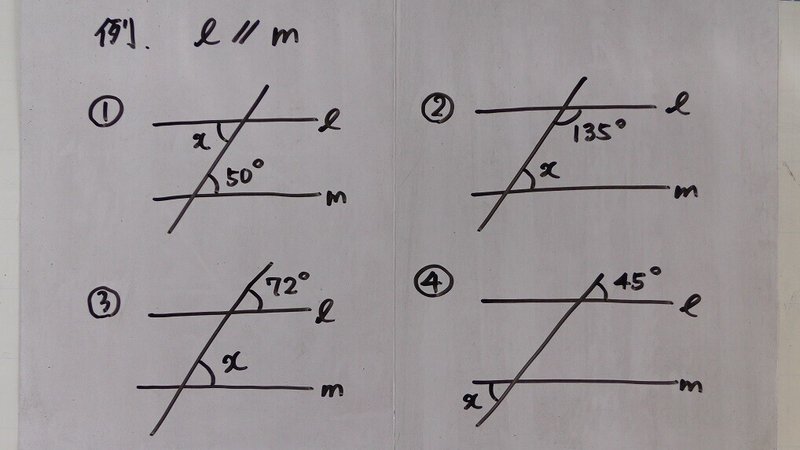



11 5 平行線の幾何 平行線の性質とその使い方 理一の数学事始め Note



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ
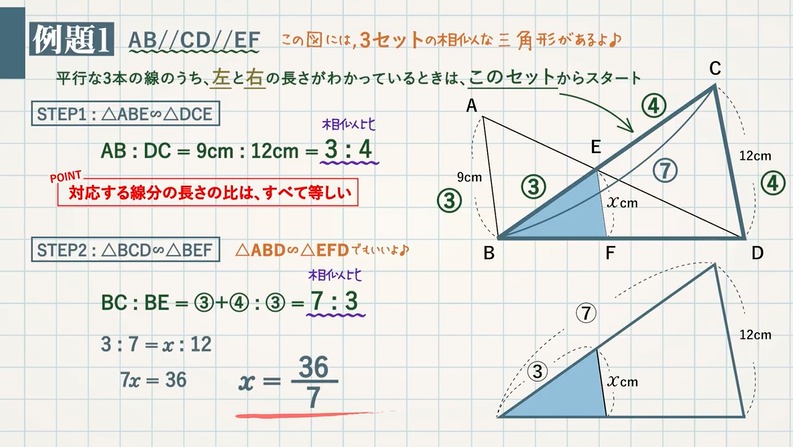



平行線と線分の比 辺の長さを求める応用問題4選 教遊者
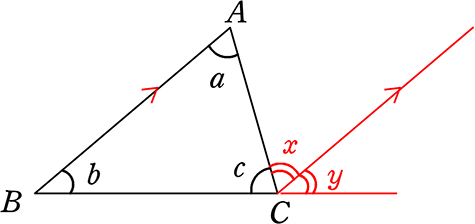



中学数学 平面図形と平行線の性質




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




中学校2年 数学 アーカイブ Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



Ten Tokyo Shoseki Co Jp Text Chu Current Sugaku Files Thema Sugaku 09 Pdf




平行四辺形の定義と性質 証明問題の解き方 数学fun
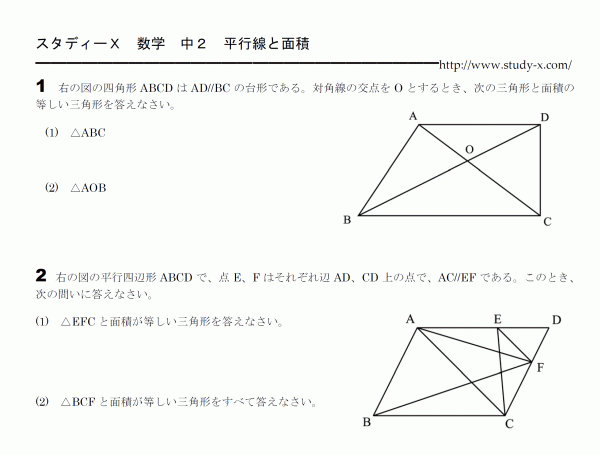



中2 数学 無料学習プリント教材
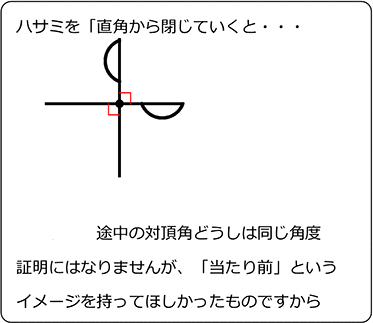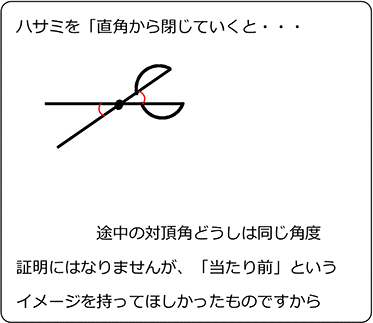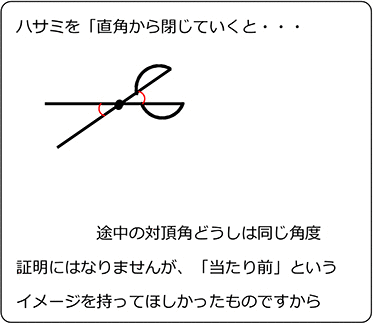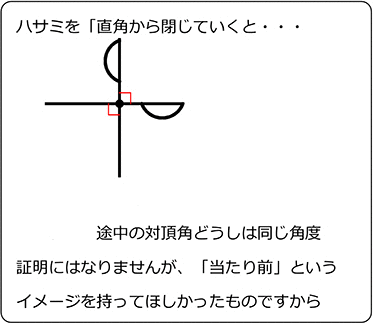



中学数学 平面図形と平行線の性質



2
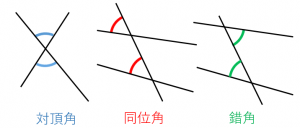



対頂角 同位角 錯角の意味を分かりやすく解説 具体例で学ぶ数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
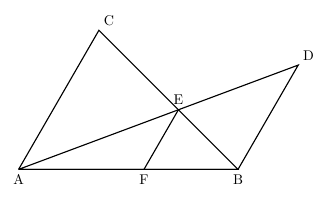



平行線の線分比の問題の解法 夢を叶える塾



平行線の同位角と錯角 中学から数学だいすき
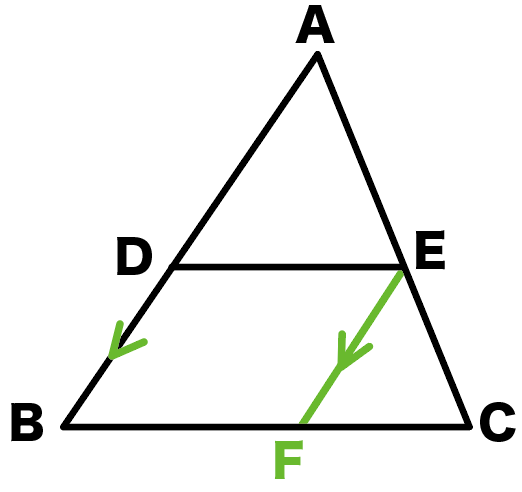



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




数学 中3 49 平行線と線分の比 基本編 Youtube




図形に関する性質の証明 身勝手な主張
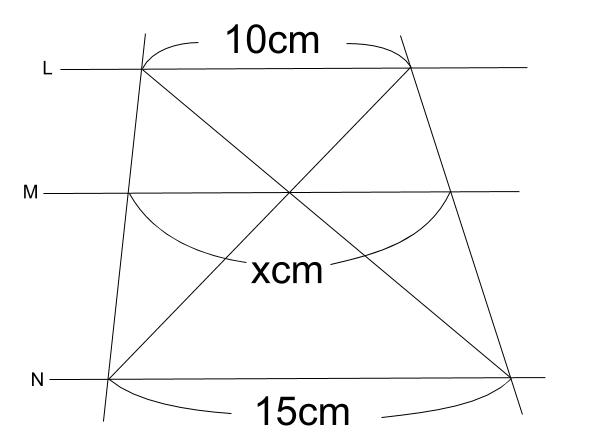



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M14 Pdf
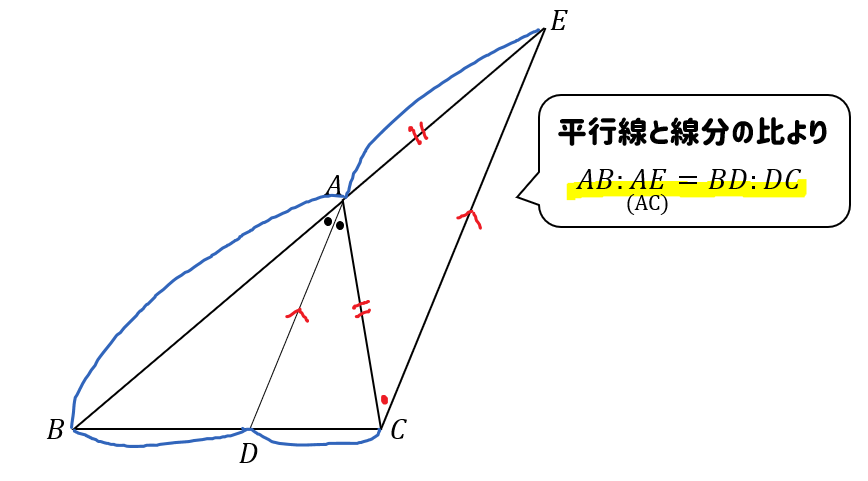



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ
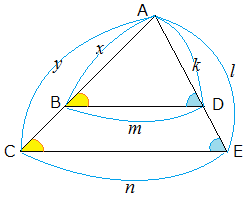



平行線と線分の比




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



Studydoctor平行線と台形 中3数学 Studydoctor
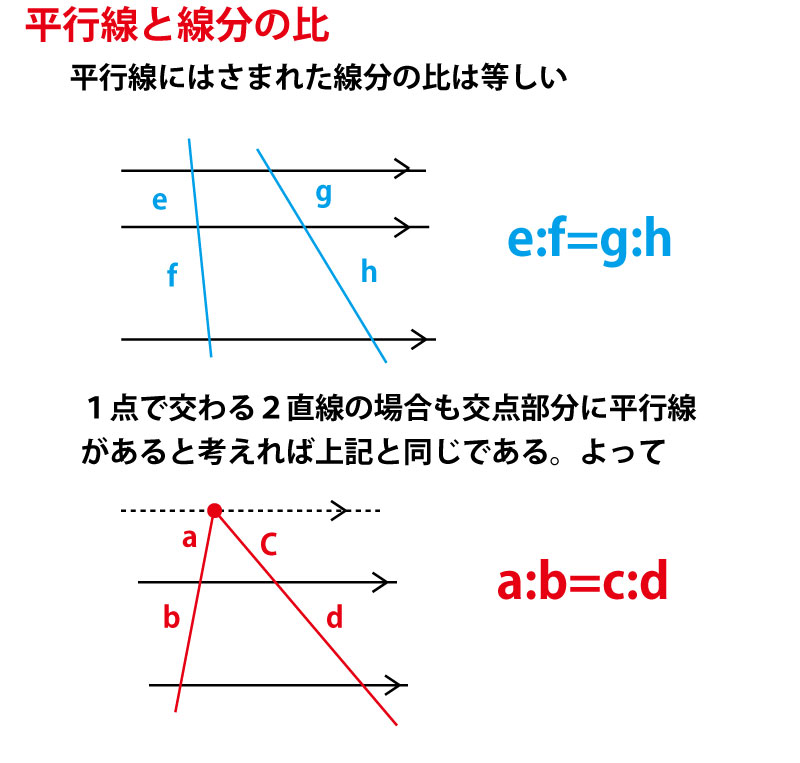



16年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




中学数学 平面図形と平行線の性質




高校数学a 平行線の性質のおさらい1 同位角 錯角 映像授業のtry It トライイット




高校数学a 平行線の性質のおさらい2 三角形 例題編 映像授業のtry It トライイット




内角の二等分線 外角の二等分線の比の定理 証明 Youtube
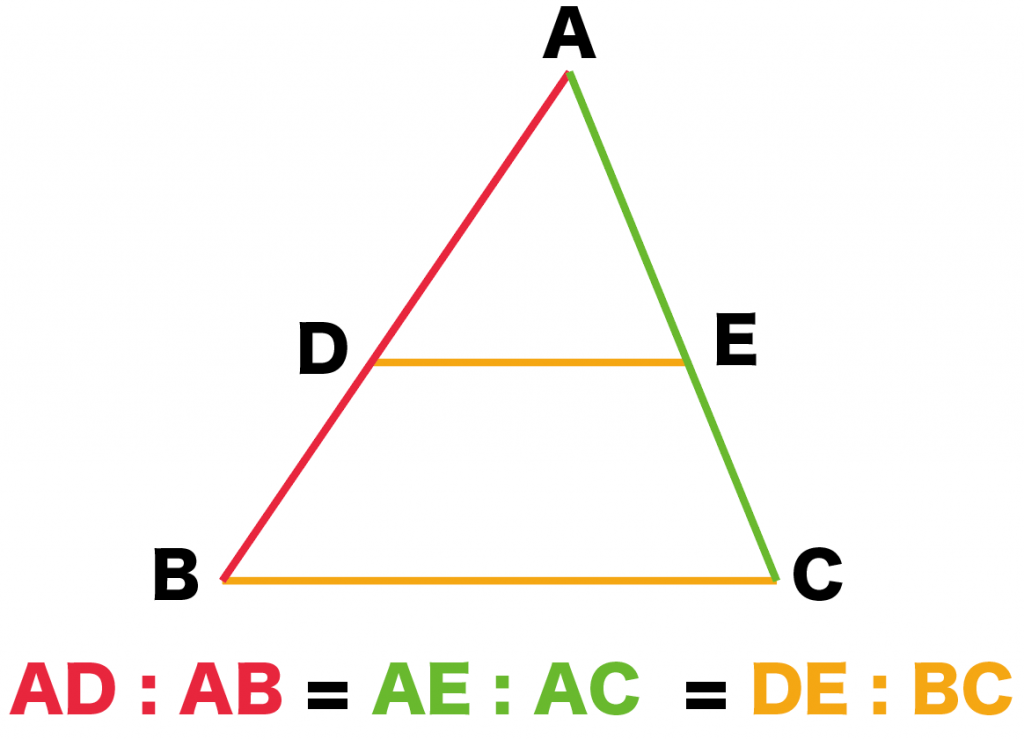



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
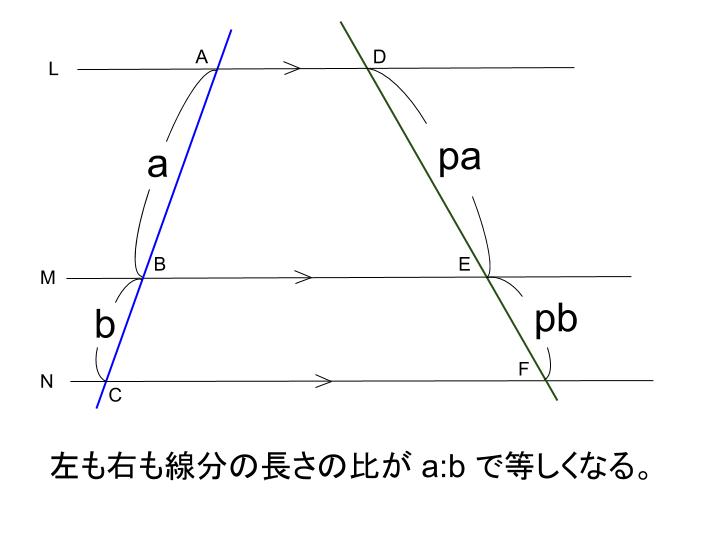



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su



中学数学証明問題で 平行線の同位角は等しい や 平行線の錯角は等しい と書 Yahoo 知恵袋




中学2年数学練習問題 平行線と面積 証明の進め方 作図の仕方
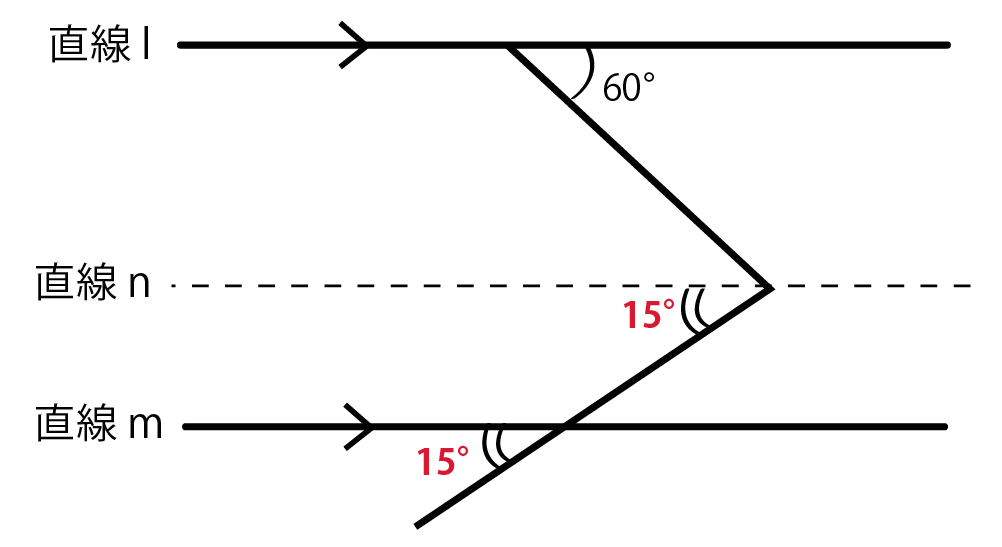



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく



Www Hokkyodai Ac Jp Files Pdf



Studydoctor平行線と線分の比の利用 中3数学 Studydoctor
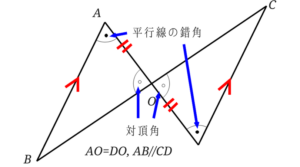



平行線の同位角や錯角が等しいことの証明 まぜこぜ情報局



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




常滑市のイチゴ狩り 朱里いちご園 朱里いちご園
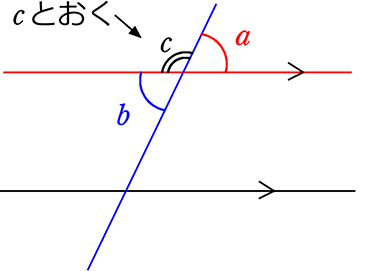



中学数学 平面図形と平行線の性質



至急 平行線と線分の比の逆の証明を教えてください Ad Db Yahoo 知恵袋




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




平行線と線分の比 の問題のわからないを5分で解決 映像授業のtry It トライイット



Studydoctor平行線の性質と証明 中2数学 Studydoctor




平行線の同位角 の証明 1 古代から数学者たちを悩ませ続けた 平行線公準 問題 アプロットの中高一貫校専門個別塾 大阪 谷町9丁目 上本町の個別指導塾



0 件のコメント:
コメントを投稿